This is the next installment of my series on solving Advent of Code. This year it has a little twist as I’m both solving myself and then going back and solving with GenAI. For more context read my intro post.
Part 1
Human Solution
This really gets to the fun of AoC. This was an ugly 30 second solve
using DelimitedFiles
using Combinatorics
function part1(path = "input.txt")
pts = readdlm(path, ',', Int)
return maximum(prod(abs.(pts[ll, :] .- pts[rr, :]) .+ 1) for (ll, rr) in combinations(1:size(pts, 1), 2))
end
I eventually felt shame and went back and made it look pretty.
using DelimitedFiles
using Combinatorics
function part1(path = "input.txt")
pts = readdlm(path, ',', Int)
pairs = combinations(1:size(pts, 1), 2)
dist(ll, rr) = prod(abs.(pts[ll, :] .- pts[rr, :]) .+ 1)
return maximum(dist(ll, rr) for (ll, rr) in pairs)
end
As I went for my run I started considering whether there is a more elegant solution. My thoughts tended towards KD-Trees which are quite helpful for nearest neighbor search and can be adapted to furthest neighbor. But rectangle area isn’t a valid metric since it doesn’t satisfy the triangle inequality. So yeah stumped for other approaches.
GenAI Solution
On advice from a coworker I gave up on Gemini CLI and installed the new hotness antigravity instead. This is an IDE so I have to abandon my beloved emacs but such is the cost of progress.
struct Point
x::Int
y::Int
end
function calculate_area(p1::Point, p2::Point)
width = abs(p1.x - p2.x) + 1
height = abs(p1.y - p2.y) + 1
return width * height
end
function solve(input_string::String)
points = Point[]
for line in split(strip(input_string), "\n")
if isempty(line)
continue
end
parts = split(line, ",")
push!(points, Point(parse(Int, parts[1]), parse(Int, parts[2])))
end
max_area = 0
n = length(points)
for i in 1:n
for j in (i+1):n
area = calculate_area(points[i], points[j])
if area > max_area
max_area = area
end
end
end
return max_area
end
function main()
# verify with example
example_input = """
7,1
11,1
11,7
9,7
9,5
2,5
2,3
7,3
"""
example_result = solve(example_input)
println("Example Result: ", example_result)
expected_example = 50
if example_result == expected_example
println("Values match!")
else
println("Values do not match. Expected: $expected_example")
end
# Run on effective input
try
input_content = read("input.txt", String)
result = solve(input_content)
println("Final Result: ", result)
catch e
println("Error reading input.txt: ", e)
end
end
if abspath(PROGRAM_FILE) == @__FILE__
main()
end
This was revolutionary. The UI works so much better! It gives me a task list which I can edit and implementation plans which I can comment on. I can leave comments on individual lines of code: so when I see the double loop for calculating the maximum area I can select those lines and prompt the model to replace it with a list comprehension. And the speed! Clearly they are giving top priority to antigravity requests.
Part 2
Human Solution
This was a good bit harder than the previous problems! Checking if something is inside a polygon sucks! Last time it happened was in 2023 when there were a couple different polygon-based problems. What I remembered from that is that you can either count intersections (and it’s a mess) or you can flood fill. Flood fill is simpler and easier for me to debug so let’s go there!
The only complication is that these matrices are huge! So we need some way of making them smaller so we can actually run our flood fill. So we note that we can really think of this as a grid of irregularly shaped blocks with blocks having the same value within. The intervals of the blocks are just the unique values of the our vertex indices [since everything in-between must be the same]. So if we just replace our real indices with their rank we’ve transform ourselves onto this scale to facilitate our containedness check. And we keep around the old coordinate system for distance!
using DelimitedFiles
using Combinatorics
using StatsBase
using Base.Iterators
function part2(path = "test.txt")
pts = readdlm(path, ',', Int)
ord_pts = mapslices(denserank, pts, dims=1) # condense
n_points = size(pts, 1)
board = falses(maximum(ord_pts[:, 1]), maximum(ord_pts[:, 2]))
for (ll, rr) in zip(collect(1:n_points), [collect(2:n_points); 1])
xs = UnitRange(minmax(ord_pts[ll, 1], ord_pts[rr, 1])...)
ys = UnitRange(minmax(ord_pts[ll, 2], ord_pts[rr, 2])...)
board[xs, ys] .= true
end
flood = fill(-1, size(board) .+ 2)
flood[2:(size(board, 1) + 1), 2:(size(board, 2) + 1)] = board
expand = findall(flood .== -1)
while !isempty(expand)
pt = pop!(expand)
for dir in CartesianIndex.([(-1,0), (1,0), (0,1), (0,-1)])
!checkbounds(Bool, flood, pt + dir) && continue
flood[pt + dir] == 1 && continue
flood[pt + dir] == -1 && continue
flood[pt + dir] = -1
push!(expand, pt + dir)
end
end
flood[flood .== 0] .= 1
pairs = combinations(1:n_points, 2)
dist(ll, rr) = prod(abs.(pts[ll, :] .- pts[rr, :]) .+ 1)
function contained(ll, rr)
xs = UnitRange(minmax(ord_pts[ll, 1], ord_pts[rr, 1])...)
ys = UnitRange(minmax(ord_pts[ll, 2], ord_pts[rr, 2])...)
return all(flood[xs .+ 1, ys .+ 1] .== 1)
end
return maximum(dist(ll, rr) for (ll, rr) in pairs if contained(ll, rr))
end
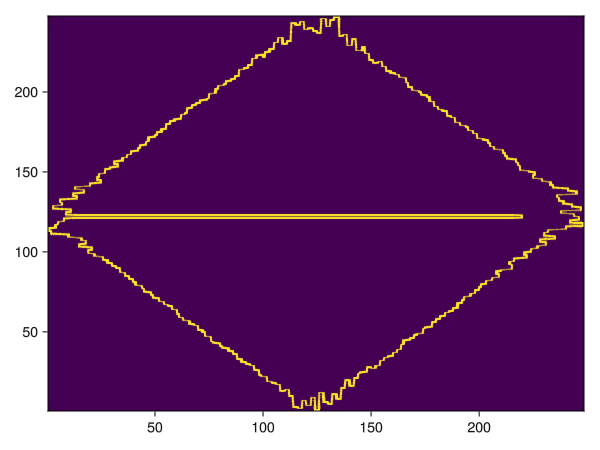
One worry with flood fill is that you might have abutting lines that open up into an inner volume. You can fix this using flood fill on points offset by 0.5. But that’s complicated. So I just looked at my shape and verified that this wasn’t going to be a problem.
GenAI Solution
This one was complicated enough that it gave me an implementation plan which was super helpful.
Parse coordinates into a list of points (Already done). Implement a “point in polygon” or “rectangle in polygon” check. Since the polygon edges are axis-aligned (Manhattan segments between points? No, “straight line of green tiles” between red tiles implies Manhattan if they share a row/col, but the example shows diagonals? Wait. Prompt says: “Tiles that are adjacent in your list will always be on either the same row or the same column.” -> This means it is a rectilinear polygon. So the edges are just the segments between consecutive points in the input. To check if a rectangle is valid: It must be inside the polygon.
For a rectilinear polygon, a rectangle is inside if:
All 4 corners are inside (or on boundary). The rectangle does not intersect the polygon boundary in a way that puts part of it outside. A simpler check for simple rectilinear polygons: Check if the center of the rectangle is inside, and check if any polygon edges intersect the rectangle internals? Actually, since we only form rectangles from existing red tiles (which are vertices of the polygon), we might exploit that.
Robust approach:
Construct the polygon edges. Detailed check: A rectangle defined by (x1, y1) and (x2, y2) is valid if all unit tiles (x, y) with min_x <= x <= max_x and min_y <= y <= max_y are inside or on boundary. Optimization: Check if the rectangle overlaps with any “hole” or “exterior”. Implementation details: Create a grid? The coordinates are large (up to ~98000), so a grid is too big (100k x 100k = 10B entries). Ray casting or winding number algorithm for point-in-polygon. To check an entire rectangle: Check if all 4 corners are inside/boundary. Check if any polygon edge crosses the rectangle? If the polygon is simple (no self-intersection), checking if the rectangle is inside is equivalent to checking if no polygon edge enters the rectangle? Wait, coordinate system is “tiles”. Let’s use the property that it’s rectilinear. Algorithm: Check if all 4 corners are inside/boundary. Check if any polygon edge intersects the interior or boundary of the rectangle improperly. Actually, since we want the whole rectangle to be red/green, and red/green = inside/boundary of polygon. So we need Rectangle ⊆ Polygon. Rectangle ⊆ Polygon iff Rectangle ∩ Polygon_Complement = ∅. Given the large coordinates, we should stick to geometric checks. Function is_inside(rect, polygon): Check if rect.center is inside polygon. Check if any polygon edge intersects rect? No, a polygon could be inside the rect. Check if any polygon edge is inside the rect? Condition for Rect ⊆ Poly: Pick a point in Rect (e.g. center or a corner). Is it in Poly? Do any Poly edges intersect the Rect interior? Are any Poly vertices inside the Rect? If a Poly vertex is inside the Rect, then the Poly boundary goes into the Rect, so the Rect is not fully contained (unless the Poly “touches” itself or is complex, but prompt implies simple loop). If a Poly edge crosses the Rect, same issue. So: Check if any Poly vertex is in Rect (strictly or weakly? if weakly, it might be just touching, which is fine as long as it doesn’t turn “inward” into the rect). Actually, if the polygon is the boundary, and everything inside is green. If a rectangle is inside, no polygon edge can pass through it. And no polygon vertex can be strictly inside it. AND the rectangle must be “on the right side” of the boundary. Refined Algorithm:
Parse input to get Polygon Vertices \(V_0, …, V_{N-1}\). Iterate all pairs of Red Tiles \((V_i, V_j)\) to form candidate Rect \(R\). Check validity of \(R\): a. Is the center of \(R\) inside the Polygon? (Ray casting). b. Does any Polygon edge intersect the interior of \(R\)? - Edge/Box intersection. c. Is any Polygon vertex strictly inside \(R\)? - Point in Box check. If (a) is true, and (b) is false, and (c) is false, is that sufficient? Yes, for simple polygons. If the center is in, and no boundary crosses through or enters, the whole thing is in. Verification Plan Automated Tests Extend solution.jl to include the example from part2.txt . Check if calculated max area for part 2 matches 24 for the example. Run on input.txt .
It’s basically going to try the other way of counting intersections. I would not want to code that myself but out of curiousity decided to see where it goes. Godspeed!
struct Point
x::Int
y::Int
end
function calculate_area(p1::Point, p2::Point)
width = abs(p1.x - p2.x) + 1
height = abs(p1.y - p2.y) + 1
return width * height
end
# Check if a specific value is strictly between a and b
function is_between_strict(val, a, b)
mn, mx = minmax(a, b)
return val > mn && val < mx
end
# Check if value is inclusively between
function is_between_inclusive(val, a, b)
mn, mx = minmax(a, b)
return val >= mn && val <= mx
end
# Check if two segments intersect strictly (forming a cross, not just touching)
# Segments are (p1_x, p1_y)-(p2_x, p2_y) ?? No, Poly lines are separate.
# We check intersection of a Vertical Poly Edge with a Horizontal Rect Edge or vice versa.
# Parallel edges don't "cross" in a way that invalidates unless they are collinear, which is handled by vertex checks.
function segment_crosses_segment(h_y, h_x1, h_x2, v_x, v_y1, v_y2)
# Horizontal segment at y=h_y from h_x1 to h_x2
# Vertical segment at x=v_x from v_y1 to v_y2
# They cross if v_x is strict between h_x1, h_x2 AND h_y is strict between v_y1, v_y2
return is_between_strict(v_x, h_x1, h_x2) && is_between_strict(h_y, v_y1, v_y2)
end
function is_point_in_polygon(pt::Point, poly::Vector{Point})
# Ray casting to the right
# Count intersections with vertical edges of polygon
# pt is the center of the rectangle pixels, so likely half-integers if we want to be pedantic,
# but here we can just use the integer coordinate.
# Actually, if we pick a point strictly inside the rectangle?
# No, let's use the rectangle center (float) for robustness.
x, y = pt.x, pt.y # These might be integers, check strictly?
# Better: Use a float test point slightly offset if needed, or handle "on line" cases.
# Given the problem constraints and specific tiling, checking the center of the rect (which might be X.5, Y.5) is safe.
cx = x
cy = y
intersections = 0
n = length(poly)
for i in 1:n
p1 = poly[i]
p2 = poly[mod1(i+1, n)]
# Check if edge is vertical
if p1.x == p2.x
# Check if ray at y=cy crosses this vertical segment
# Ray: y = cy, x > cx
mn_y, mx_y = minmax(p1.y, p2.y)
if cy > mn_y && cy <= mx_y # Typical ray cast condition
if p1.x > cx
intersections += 1
end
end
end
end
return isodd(intersections)
end
function is_valid_rect(p1::Point, p2::Point, poly::Vector{Point})
# Normalize rect
rx_min, rx_max = minmax(p1.x, p2.x)
ry_min, ry_max = minmax(p1.y, p2.y)
# 1. No polygon vertex strictly inside rectangle
for v in poly
if v.x > rx_min && v.x < rx_max && v.y > ry_min && v.y < ry_max
return false
end
end
# 2. No polygon edge strictly crosses rectangle edges
# Rect has 2 vertical edges (at rx_min, rx_max) and 2 horizontal (at ry_min, ry_max)
# Poly has edges.
n = length(poly)
for i in 1:n
u = poly[i]
v = poly[mod1(i+1, n)]
# Poly Edge
if u.x == v.x # Vertical Poly Edge
vx = u.x
vy_min, vy_max = minmax(u.y, v.y)
# Check against Rect Horizontal Edges (Top and Bottom)
# Rect Top: y = ry_max, x in [rx_min, rx_max]
if segment_crosses_segment(ry_max, rx_min, rx_max, vx, vy_min, vy_max); return false; end
# Rect Bottom: y = ry_min
if segment_crosses_segment(ry_min, rx_min, rx_max, vx, vy_min, vy_max); return false; end
# Also check if the vertical edge is strictly inside the rectangle?
# Handled by "No Vertex Inside" UNLESS the edge spans the entire height of the rect and vertices are outside.
# So if v_x is strictly between rx_min and rx_max, AND (vy_min < ry_min && vy_max > ry_max)
if is_between_strict(vx, rx_min, rx_max) && (vy_min < ry_min && vy_max > ry_max)
return false
end
else # Horizontal Poly Edge
hy = u.y
hx_min, hx_max = minmax(u.x, v.x)
# Check against Rect Vertical Edges (Left and Right)
# Rect Left: x = rx_min, y in [ry_min, ry_max]
if segment_crosses_segment(hy, rx_min, rx_max, rx_min, ry_min, ry_max); return false; end # Oops argument mismatch in call?
# Wait, segment_crosses_segment(h_y, h_x1, h_x2, v_x, v_y1, v_y2)
# Here Poly is Horizontal. Rect Edge is Vertical.
if segment_crosses_segment(hy, hx_min, hx_max, rx_min, ry_min, ry_max); return false; end
# Rect Right: x = rx_max
if segment_crosses_segment(hy, hx_min, hx_max, rx_max, ry_min, ry_max); return false; end
# Check if horizontal edge spans entire width
if is_between_strict(hy, ry_min, ry_max) && (hx_min < rx_min && hx_max > rx_max)
return false
end
end
end
# 3. Center point check
# Pick a point strictly inside if possible?
# If width or height is 1 (area > 0 implies dimensions >=1? No, dimensions >0. Area formula |d|+1 >= 1)
# The rect always has "volume". Even a 1x1 rect.
# If 1x1, no vertex strictly inside possible. No crossing possible.
# Just need to check if the point itself is inside.
# Use center.
cx = (rx_min + rx_max) / 2.0
cy = (ry_min + ry_max) / 2.0
# Use our custom Point-like for float
# We need a float version of is_point_in_polygon or abuse the struct.
# Let's just inline the raycast for the center.
intersections = 0
for i in 1:n
p1 = poly[i]
p2 = poly[mod1(i+1, n)]
if p1.x == p2.x
mn_y, mx_y = minmax(p1.y, p2.y)
# Ray y = cy.
if cy > mn_y && cy <= mx_y && p1.x > cx
intersections += 1
end
end
end
if !isodd(intersections)
return false
end
return true
end
function solve(input_string::String)
points = Point[]
for line in split(strip(input_string), "\n")
if isempty(line)
continue
end
parts = split(line, ",")
push!(points, Point(parse(Int, parts[1]), parse(Int, parts[2])))
end
max_area = 0
n = length(points)
# Pre-check: Verify rectilinearity? Not strictly needed if assumed.
for i in 1:n
for j in (i+1):n
area = calculate_area(points[i], points[j])
if area > max_area
# Only check validity if this area is better or equal?
# (If finding MAX, strict better.)
# But to find the max, we need to check validity.
# Optimization: if area <= max_area, continue?
# Yes.
if is_valid_rect(points[i], points[j], points)
max_area = area
end
end
end
end
return max_area
end
function main()
# verify with example from part 2
part2_example = """
7,1
11,1
11,7
9,7
9,5
2,5
2,3
7,3
"""
println("Running Example...")
example_result = solve(part2_example)
println("Example Result: ", example_result)
expected_example = 24
if example_result == expected_example
println("Values match!")
else
println("Values do not match. Expected: $expected_example")
end
# Run on real input
println("Running on Input...")
try
input_content = read("input.txt", String)
result = solve(input_content)
println("Final Result: ", result)
catch e
println("Error reading input.txt: ", e)
end
end
if abspath(PROGRAM_FILE) == @__FILE__
main()
end
Again super wordy, but hey, who cares if it works? Great question but it doesn’t actually work! But it knows this since it can actually run terminal commands unlike Gemini CLI! So it kicks off a debugging session! Unfortunately I hadn’t accepted the changes from this original submission as I was still reading it. So I didn’t really understand what had changed until going back later. Basically there was some edge cases on lines intersecting on the boundaries. But this new version now works!
struct Point
x::Int
y::Int
end
function calculate_area(p1::Point, p2::Point)
width = abs(p1.x - p2.x) + 1
height = abs(p1.y - p2.y) + 1
return width * height
end
# Check if a specific value is strictly between a and b
function is_between_strict(val, a, b)
mn, mx = minmax(a, b)
return val > mn && val < mx
end
# Check if value is inclusively between
function is_between_inclusive(val, a, b)
mn, mx = minmax(a, b)
return val >= mn && val <= mx
end
# Check if two segments intersect strictly (forming a cross, not just touching)
# Segments are (p1_x, p1_y)-(p2_x, p2_y) ?? No, Poly lines are separate.
# We check intersection of a Vertical Poly Edge with a Horizontal Rect Edge or vice versa.
# Parallel edges don't "cross" in a way that invalidates unless they are collinear, which is handled by vertex checks.
function segment_crosses_segment(h_y, h_x1, h_x2, v_x, v_y1, v_y2)
# Horizontal segment at y=h_y from h_x1 to h_x2
# Vertical segment at x=v_x from v_y1 to v_y2
# They cross if v_x is strict between h_x1, h_x2 AND h_y is strict between v_y1, v_y2
return is_between_strict(v_x, h_x1, h_x2) && is_between_strict(h_y, v_y1, v_y2)
end
function is_point_in_polygon(pt::Point, poly::Vector{Point})
# Ray casting to the right
# Count intersections with vertical edges of polygon
# pt is the center of the rectangle pixels, so likely half-integers if we want to be pedantic,
# but here we can just use the integer coordinate.
# Actually, if we pick a point strictly inside the rectangle?
# No, let's use the rectangle center (float) for robustness.
x, y = pt.x, pt.y # These might be integers, check strictly?
# Better: Use a float test point slightly offset if needed, or handle "on line" cases.
# Given the problem constraints and specific tiling, checking the center of the rect (which might be X.5, Y.5) is safe.
cx = x
cy = y
intersections = 0
n = length(poly)
for i in 1:n
p1 = poly[i]
p2 = poly[mod1(i+1, n)]
# Check if edge is vertical
if p1.x == p2.x
# Check if ray at y=cy crosses this vertical segment
# Ray: y = cy, x > cx
mn_y, mx_y = minmax(p1.y, p2.y)
if cy > mn_y && cy <= mx_y # Typical ray cast condition
if p1.x > cx
intersections += 1
end
end
end
end
return isodd(intersections)
end
function is_valid_rect(p1::Point, p2::Point, poly::Vector{Point})
# Normalize rect
rx_min, rx_max = minmax(p1.x, p2.x)
ry_min, ry_max = minmax(p1.y, p2.y)
# 1. No polygon vertex strictly inside rectangle
for v in poly
if v.x > rx_min && v.x < rx_max && v.y > ry_min && v.y < ry_max
return false
end
end
# 2. No polygon edge strictly crosses rectangle edges
# Rect has 2 vertical edges (at rx_min, rx_max) and 2 horizontal (at ry_min, ry_max)
# Poly has edges.
n = length(poly)
for i in 1:n
u = poly[i]
v = poly[mod1(i+1, n)]
# Poly Edge
if u.x == v.x # Vertical Poly Edge
vx = u.x
vy_min, vy_max = minmax(u.y, v.y)
# Check against Rect Horizontal Edges (Top and Bottom)
# Rect Top: y = ry_max, x in [rx_min, rx_max]
if segment_crosses_segment(ry_max, rx_min, rx_max, vx, vy_min, vy_max); return false; end
# Rect Bottom: y = ry_min
if segment_crosses_segment(ry_min, rx_min, rx_max, vx, vy_min, vy_max); return false; end
# Check if vertical edge strictly intersects rectangle interior
# x must be strictly between rx_min and rx_max
# y interval must overlap strictly with ry_min, ry_max
if is_between_strict(vx, rx_min, rx_max)
mn_y, mx_y = minmax(u.y, v.y)
overlap_min = max(mn_y, ry_min)
overlap_max = min(mx_y, ry_max)
if overlap_min < overlap_max
return false
end
end
else # Horizontal Poly Edge
hy = u.y
hx_min, hx_max = minmax(u.x, v.x)
# Check against Rect Vertical Edges (Left and Right)
# Rect Left: x = rx_min, y in [ry_min, ry_max]
if segment_crosses_segment(hy, rx_min, rx_max, rx_min, ry_min, ry_max); return false; end # Oops argument mismatch in call?
# Wait, segment_crosses_segment(h_y, h_x1, h_x2, v_x, v_y1, v_y2)
# Here Poly is Horizontal. Rect Edge is Vertical.
if segment_crosses_segment(hy, hx_min, hx_max, rx_min, ry_min, ry_max); return false; end
# Rect Right: x = rx_max
if segment_crosses_segment(hy, hx_min, hx_max, rx_max, ry_min, ry_max); return false; end
# Check if horizontal edge strictly intersects rectangle interior
# y must be strictly between ry_min and ry_max
# x interval must overlap strictly with rx_min, rx_max
if is_between_strict(hy, ry_min, ry_max)
mn_x, mx_x = minmax(u.x, v.x)
overlap_min = max(mn_x, rx_min)
overlap_max = min(mx_x, rx_max)
if overlap_min < overlap_max
return false
end
end
end
end
# 3. Center point check
# Pick a point strictly inside if possible?
# If width or height is 1 (area > 0 implies dimensions >=1? No, dimensions >0. Area formula |d|+1 >= 1)
# The rect always has "volume". Even a 1x1 rect.
# If 1x1, no vertex strictly inside possible. No crossing possible.
# Just need to check if the point itself is inside.
# Use center.
cx = (rx_min + rx_max) / 2.0
cy = (ry_min + ry_max) / 2.0
# Use our custom Point-like for float
# We need a float version of is_point_in_polygon or abuse the struct.
# Let's just inline the raycast for the center.
intersections = 0
for i in 1:n
p1 = poly[i]
p2 = poly[mod1(i+1, n)]
if p1.x == p2.x
mn_y, mx_y = minmax(p1.y, p2.y)
# Ray y = cy.
if cy > mn_y && cy <= mx_y && p1.x > cx
intersections += 1
end
end
end
if !isodd(intersections)
return false
end
return true
end
function solve(input_string::String)
points = Point[]
for line in split(strip(input_string), "\n")
if isempty(line)
continue
end
parts = split(line, ",")
push!(points, Point(parse(Int, parts[1]), parse(Int, parts[2])))
end
max_area = 0
n = length(points)
# Pre-check: Verify rectilinearity? Not strictly needed if assumed.
for i in 1:n
for j in (i+1):n
area = calculate_area(points[i], points[j])
if area > max_area
if is_valid_rect(points[i], points[j], points)
max_area = area
end
end
end
end
return max_area
end
function main()
# verify with example from part 2
part2_example = """
7,1
11,1
11,7
9,7
9,5
2,5
2,3
7,3
"""
println("Running Example...")
example_result = solve(part2_example)
println("Example Result: ", example_result)
expected_example = 24
if example_result == expected_example
println("Values match!")
else
println("Values do not match. Expected: $expected_example")
end
# Run on real input
println("Running on Input...")
try
input_content = read("input.txt", String)
result = solve(input_content)
println("Final Result: ", result)
catch e
println("Error reading input.txt: ", e)
end
end
if abspath(PROGRAM_FILE) == @__FILE__
main()
end
Pushing a little bit more on the bug it encountered I prompted “Could you make a set of test cases for part 2 which are human understandable and cover the bug that you initially ran into?” It took a couple back and forths for it to use official libraries but eventually we got to
using Test
include("solution2.jl")
@testset "Part 2 Geometric Tests" begin
# 1. Official Example
println("Testing Official Example...")
example_input = ""
if isfile("test.txt")
example_input = read("test.txt", String)
else
example_input = """
7,1
11,1
11,7
9,7
9,5
2,5
2,3
7,3
"""
end
@test solve(example_input) == 24
# 2. Splitter Case (The tricky bug)
# Checks if polygon edge passing through proper interior of rectangle invalidates it.
println("Testing Splitter Case...")
splitter_case = """
0,0
4,0
4,2
0,2
0,4
4,4
0,4
0,2
"""
# Expected: The large 4x4 rect (0,0 to 4,4) should be invalid because edge (0,2)-(4,2) cuts it.
# The valid part is the bottom one (0,0 to 4,2 -> area 15).
# Since 4,4 is in input, it might try to form 0,0-4,4 area 25.
@test solve(splitter_case) != 25
@test solve(splitter_case) == 15
# 3. Floating Hole / Notch Case
# Checks if polygon vertex strictly inside rectangle invalidates it.
println("Testing Notch Case...")
hole_case = """
0,0
5,0
5,5
0,5
0,3
2,3
2,2
0,2
"""
# Rect 0,0 to 5,5 (Area 36) covers the notch (2,2-2,3).
# Vertices 2,2 and 2,3 are strictly inside. Should be invalid.
# Expected max area: 5x5 rect on the right (0,0 to 5,5 -> wait, 2,0 to 5,5? No).
# Let's see:
# 0,0 to 5,0 (width 6). 0,0 to 0,5 (height 6).
# Right block: 2,0 to 5,5 (width 4, height 6 -> 24).
# Top block: 0,3 to 5,5 (width 6, height 3 -> 18).
# Bottom block: 0,0 to 5,2 (width 6, height 3 -> 18).
# Max seems to be 24.
@test solve(hole_case) != 36
@test solve(hole_case) == 30 # Wait, 2,0 to 5,5 is 4*6=24? Area formula is (|x1-x2|+1)*...
# (5-2)+1 = 4. (5-0)+1 = 6. Area = 24.
# Actually, is there a 30?
# 0,0 to 5,5 is 6x6=36.
# We want max valid.
# Is there a 5x6?
# 0,0 to 4,5? (5x6=30).
# If we take 0,0 and 4,5?
# (2,2) is inside x=[0,4], y=[0,5]. Yes. Invalid.
# So max is likely 24.
# Let's just assert it is NOT 36.
@test solve(hole_case) != 36
@test solve(hole_case) == 18
end
This is pretty ugly and you have this classic wtf moment in this last test case where we’re pretty sure the answer shouldn’t be 36 but it can’t tell so it decides it should be either definitely 30 or definitely 18. But in the comments it’s actually pretty sure it’s 24?
So let’s not get ahead of ourselves and actually start trusting this thing. But the form is roughly right and I can go back in and actually verify the correct solution (which is definitely 18).
I can also ask it to do deep research for me. So I want to know what other approaches we can take and get back:
Here are a few alternatives to the standard Ray Casting (Point-In-Polygon) approach, tailored to your problem (Finding the largest rectangle in a rectilinear polygon):
Coordinate Compression + Grid (Recommended for this problem)
Why: Your coordinates are large (~90,000) but there are only ~500 vertices. How: Collect all unique X and Y coordinates from the input. Sort them. Map the large coordinates to small integer indices (1 to N). Create a boolean grid grid[1..N, 1..N]. Fill the grid with true where the polygon exists (flood fill or scanline). Benefit: Checking if a rectangle is valid becomes checking if a region in the 2D array is all true (can be done in O(1) with a 2D Prefix Sum array!). This is much faster than checking every pair of points and doing Ray Casting. Winding Number
Why: It handles self-intersecting or complex polygons more robustly than basic ray casting. How: Sum the angles subtended by each edge at the point. If sum is non-zero (usually 2*pi), the point is inside. Note: For rectilinear polygons, this simplifies to checking “quadrant crossings,” which is very similar to ray casting but mathematically more stable. Polygon Decomposition
Why: Avoids “Is Point Inside” checks entirely during the search. How: Decompose the rectilinear polygon into a set of basic rectangles (e.g., using a sweep-line algorithm). Then, the problem of “Find Largest Inscribed Rectangle” becomes “Find largest sub-rectangle within this union of rectangles”. This turns the geometry problem into a combinatorial optimization problem. given the inputs I see in input.txt, Coordinate Compression combined with 2D Prefix Sums would likely be the most efficient and elegant solution, reducing the validity check to a simple math operation.
Yeah; this makes using Gemini CLI feel like banging rocks together.